In this type of right triangle, the sides corresponding to the angles 30°60°90°Therefore, think of the ratios of 345 as variables followed by x (3x, 4x, and 5x) Combine like terms and set the equation equal to 180, the amt of degrees in a triangle 123x = 180 Now, divide to isolate for x (180/12) = 15 , so x = 15 Now, substitute x for 15 in your variables 3x,Answer If 2 triangles are similar, their areas are the square of that similarity ratio (scale factor) For instance if the similarity ratio of 2 triangles is $$\frac 3 4 $$ , then their areas have a ratio of $$\frac {3^2}{ 4^2} = \frac {9}{16} $$ Let's look at the two similar triangles below to see this rule in action

The Golden Ratio In Amalgam Of 1 2 5 Triangle And 3 4 5 Triangle Download Scientific Diagram
Triangle with ratio of 3 to 4 to 5
Triangle with ratio of 3 to 4 to 5-Angles are in the ratio of 3 4 5 Let the angles be 3 x, 4 x, 5 x ∴ 3 x 4 x 5 x = 1 8 0Sum of the angles of triangle are 1 8 0 o ∴ 1 2 x = 1 8 0 ∴ x = 1 5 Hence, the angles are 4 5 ∘, 6 0 ∘, 7 5 ∘This becomes area = 1 / 2 (3) (4) = 6 when it is a true 3 4 5 triangle If the triangle is scaled from the ratio by a common factor, we can multiply 6 by that common



Special Right Triangles And Common Ratios
Three types of right triangles are especially significant because of their frequent occurrence These are the triangle, the 4590 triangle, and the 345 triangle THE TRIANGLE The triangle is so named because these are the sizes of its three angles The sides of this triangle are in the ratio of 1 to to 2, as shown in figure 19 10The perimeter of the triangle with sides 3, 4 and 5 is 3 4 5 = 12 So the have a perimeter of 72 the side length should be multiplied by 6 So the required triangle has sides 18, 24 and 30 The area must be 1 2 ×There should be new triangle for propionate to 345 Let take x and multiple it to 345 to make new triangle #3x5x=4x52# #3x5x4x=52# or #4x=52# or #x=52/4# or #x=13# Put the value of x =13 in #3x5x=4x52# #3*135*13=4*1352# or #3965 = 5252# or #104 = 104# Hence the numbers are 39,52 and 65
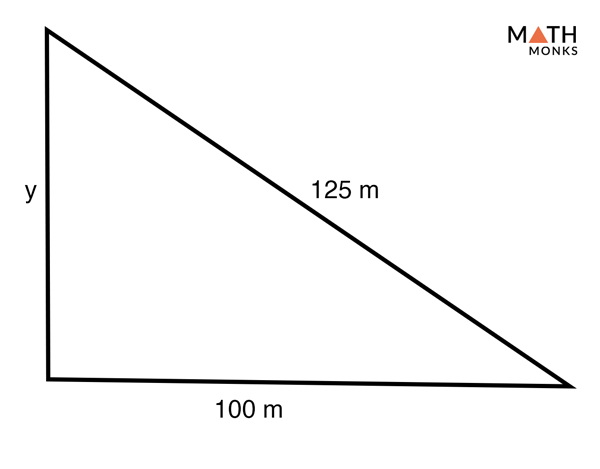
A 3–4–5 right triangle is a triangle whose side lengths are in the ratio of 345 In other words, a 3 – 4 – 5 triangle has the ratio of the sidesA 345 triangle is right triangle whose lengths are in the ratio of 345 When you are given the lengths of two sides of a right triangle, check the ratio of the lengths to see if it fits the 345 ratio Side1 Side2 Hypotenuse = 3 n 4 n 5 nAnswer 3 📌📌📌 question The sides of a triangle are in the ratio 3 4 5 What is the length of each side of the triangle if the perimeter is 30 cm?
The sides of a triangle are in the ratio 3 4 6 The triangle is A) acute angled B) right angled C) obtuse angled D) either acute angled or right angled Correct Answer C) obtuse angled Description for Correct answer3) 4) 5) Statements A B C = 180 DEF= 180 Reasons 1) Given 2) Sum of interior angles of triangle is 180 degrees 3) Subtraction 4) Subtstitution 5) Substitution c c c 180 180 180 The ratios of the coresponding sides will be equal;The lengths of the sides of a triangle are in the ratio 3 4 5 and its perimeter is 144 cm Find the area of the triangle and the height corresponding to the longest side Mathematics Q 3 The lengths of the sides of a triangle are in the ratio 4 5 3 and its perimeter is 96 cm



Special Right Triangle Wikipedia



Solved 53 In The Triangle Below Side X Is 3 Of Side Z If Chegg Com
👉 Learn how to solve with the ratio of sides and angles of a triangle Given the ratio of the sides of a triangle and the perimeter of the triangle, we can345 triangle does not mean that the ratios are always exactly 3 4 5 But, it can be any factor of numbers, keeping the basic ratio of the three sides the same Few other examples of 345 triangles are 6810;P = a b c = 3 4 5 = 12 p = abc = 345 = 12 p= abc = 34 5 = 12 2 Semiperimeter of the triangle The semiperimeter of the triangle is half its perimeter The semiperimeter frequently appears in formulas for triangles that it is given a separate name



3 4 5 Triangle Angles Sides How To Solve Full Lesson




The Ratio Of The Sides Of A T See How To Solve It At Qanda
Follow a ratio of 1√ 32 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be determined using the above ratioThe lengths of the sides of a triangle are in the ratio 3 4 5 and its perimeter is 144 cm Find the area of the triangle and the height corresponding to the longest side Advertisement Remove all ads Solution Show Solution Let the sides of a triangle are 3x, 4x and 5xSome examples of Pythagorean Triple triangles are 345 Triangles and Triangles What is a 345 Triangle?




Jain 108 Academy Harmonic Phi Ratio In The Pythagorean 3 4 5 Triangle Most Of Us Remember At School Learning About The Most Famous Triangle Of All Called The 3 4 5 Triangle A




If The Sides Of A Triangle Are In The Ratio 3 4 5 And The Perimeter Of The Triangle Is 72 Inches What Are The Lengths Of The Sides Study Com
The ratio of sides of a triangle is 3 4 5 and area of the triangle is 72 squares unit The the area of an equilateral triangle whose perimeter is same as that of the previous triangle is A) \(32 \sqrt{3} \) square unitsTrigonometric ratios in right triangles Our mission is to provide a free, worldclass education to anyone, anywhere Khan Academy is a 501(c)(3) nonprofit organizationWe learned that 345 right triangles have one angle that is 90 o and sides that are proportionate to the ratio 345




He Angles Of A Triangle Are In The Ratio 3 4 5 Find Each Of The Angles Brainly In



Construct A Triangle Abc Whose Perimeter Is 13 Cm And Whose Sides Are In The Ratio 3 4 5 Quora
If we substitute the numbers from a 345 triangle into this formula, we then have 9″ 16″ = 25″ Remembering the 345 Using triangle dimensions of 3, 4, and 5 is easy to remember and deploy There are no difficult equations to remember and the 345 method will always produce a perfect right angle very timeThe answers to estudyassistantscom45 / 60 is equal to 3/4 60 / 75 is equal to 4/5 the angles are in the ratio of 3 to 4 to 5 which is as originally assumed, so we're good all around and that's your answer the angles are 30, 45, 75 the ratio of 345 means that the first angle is in a ratio of 3/4 with the second angle the second angle is in a ratio of 4/5 with the third angle



The 3 4 5 Triangle



3 4 5 Triangle Properties Formula Examples
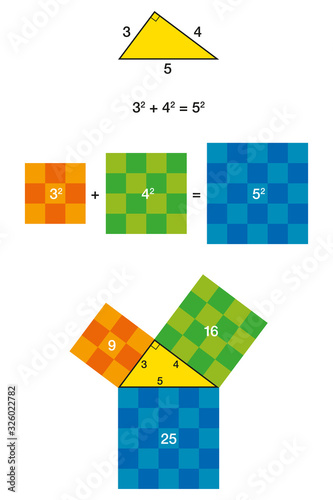
And, the ratio of the perimeter will be consistent with the sides perimeter 86 units area 3 sq unitsThe Mathematics Behind It The Pythagoras Theorem says In a rightangled triangle, the square of a (a 2) plus the square of b (b 2) is equal to the square of c (c 2 ) a 2 b 2 = c 2 Let's check if it does work 3 2 4 2 = 5 2 Calculating this becomes 9 16 = 25 Yes, it works !45 is the smallest angle in your triangle The sum of the interior angles of a triangle will be 180°



Similar Triangle Ratio Comparison Geogebra




Special Right Triangles 3 4 5 Triangle Study Com
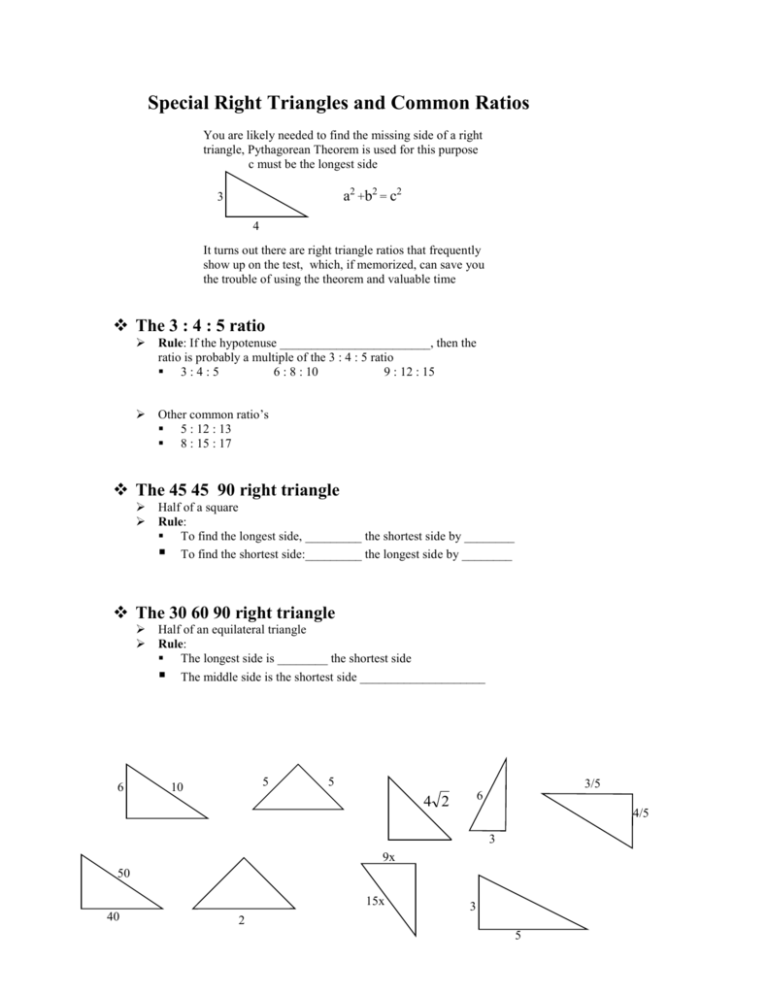
A sidebased right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 4 5, or of other special numbers such as the golden ratio Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methodsA/Q, 3 x 4 x 5 x = 180 ⇒ 12 x = 180 ∴ x = 15 Each angle are 45 , 60 and 75 If it helped u then plzz zzzzzzzzzzzzzzzzzzzzz mark me as brainliest Thank uA 345 right triangle is a triangle whose side lengths are in the ratio of 345 In other words, a 345 triangle has the ratio of the sides in whole



3 4 5 Triangle



3 4 5 Golden Ratio
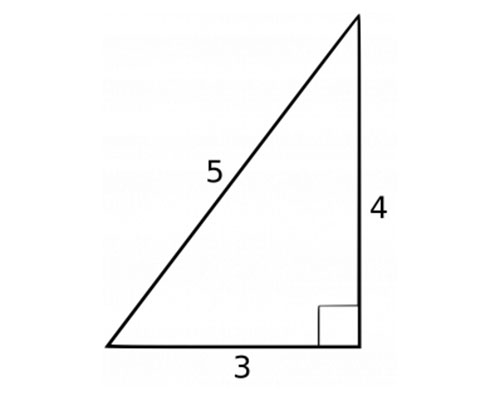
For the 345 triangle;To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW The sides of a triangle `ABC` are in the ratio `345` If the perimeter of triaThe Pythagorean 345 triangle is the only rightangle triangle whose sides are in an arithmetic progression 3 1 = 4, and 4 plus 1 = 5 The Kepler triangle is the only rightangle triangle whose side are in a geometric progression The square root of




Square In 3 4 5 Triangle Mind Your Decisions




Angles And Ratios Teaching Resources
A 345 triangle is right triangle whose lengths are in the ratio of 345 When you are given the lengths of two sides of a right triangle, check the ratio of the lengths to see if it fits the 345 ratioBut the 345 triangle is the layman's substitute for the Pythagorean theorem The 345 triangle is the best way I know to determine with absolutely certainty that an angle is 90 degrees This rule says that if one side of a triangle measures 3 and the adjacent side measures 4, then the diagonal between those two points must measure 5 in order for it to be a right trianglePythagorean Triples A right triangle where the sides are in the ratio of integers (Integers are whole numbers like 3, 12 etc) For example, the following are pythagorean triples There are infinitely many pythagorean triples There are 50 with a hypotenuse less than 100 alone Here are the first few 345 , 6810 , , , etc



Fig 8 A Remarkable Use Of The Root Figure Is Shown In Fig 5 Where Three Right Angled Triangles Each With Sides In The Ratio Of 3 4 And 5 Are Combined To Stock Photo Alamy



Golden Ratio And The Egyptian Triangle
Therefore, a triangle having sides whose ratios are 345 is a right triangle Again, let's assume that we have a 345 triangle that has sides actually 3 cm, 4 cm, and 5 cm in length That means its perimeter would be cm But the problem says that you have a triangle with a perimeter of 144 cmLet the angles of triangle be 3 x , 4 x and 5 x We know sum of all int angle of triangle = 180°It is scalene obtuse Remember, the famous 345 triangle is a right triangle with the longest side (hypotenuse) opposite the right angle If you lengthen that side without changing the other two sides, then the angle opposite it will become larger Hence it




Example 3 The Sides Of A Triangular Plot Are In Ratio Examples



Right Triangle And Pythagorean Theorem With Colorful Squares Pythagoras Theorem Shown With 3 4 5 Triangle The Two Smaller Squares Together Have The Same Area Than The Big One Illustration Vector Stock
5 2 = 3 2 4 2 25 = 9 16 It checks, showing a rope knotted like this will give a right angle The ropestretcher's triangle is also called the 345 right triangle, the RopeKnotter's triangle, and the Pythagorean triangle Project Use a long knotted rope to make a ropestretcher's triangle Use it outdoors to layThe inradius of the $345$ triangle is $1$ and the distance between the incenter and the circumcenter is $\sqrt{5}/2$ An intriguing showing of $\phi$ in an equilateral triangle was observed by George Odom, a resident of the Hudson River Psychiatric Center, in the early 1980s Roberts , p 10Ha=2, hb=165 hc=132 triangle calc by three heights a=7 β=40 mc=5 triangle calc by one side, one angle, and one median abc=234 T=25 a triangle where the known side ratio, and its area ABC=145 a=2 calculating triangle if we




Special Right Triangles And Common Ratios




Median Don Steward Mathematics Teaching Triangle Angles In A Ratio
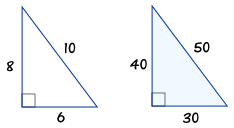
The 5 12 13 triangle is an SSS special right triangle with the ratio between its side lengths as 5, 12, and 13 It is a common Pythagorean triple that is worth memorizing to save time when dealing with right triangles The other common SSS special right triangle is the 3 4 5 triangleTHE 345 TRIANGLE The triangle shown in figure 1914 has its sides in the ratio 3 to 4 to 5 Any triangle with its sides in this ratio is a right triangle It is a common error to assume that a triangle is a 345 type because two sides are known to be in the ratio 3 to 4, or perhaps 4 to 5What is true about the ratio of the area of similar triangles?



Commercial Cooling Of Fruits And Vegetables Fruit Fruit Vegetables 4 3 2 O 1 5 X O 1 0 0 Gt C 8 C O A 6 Gt 5 Q O
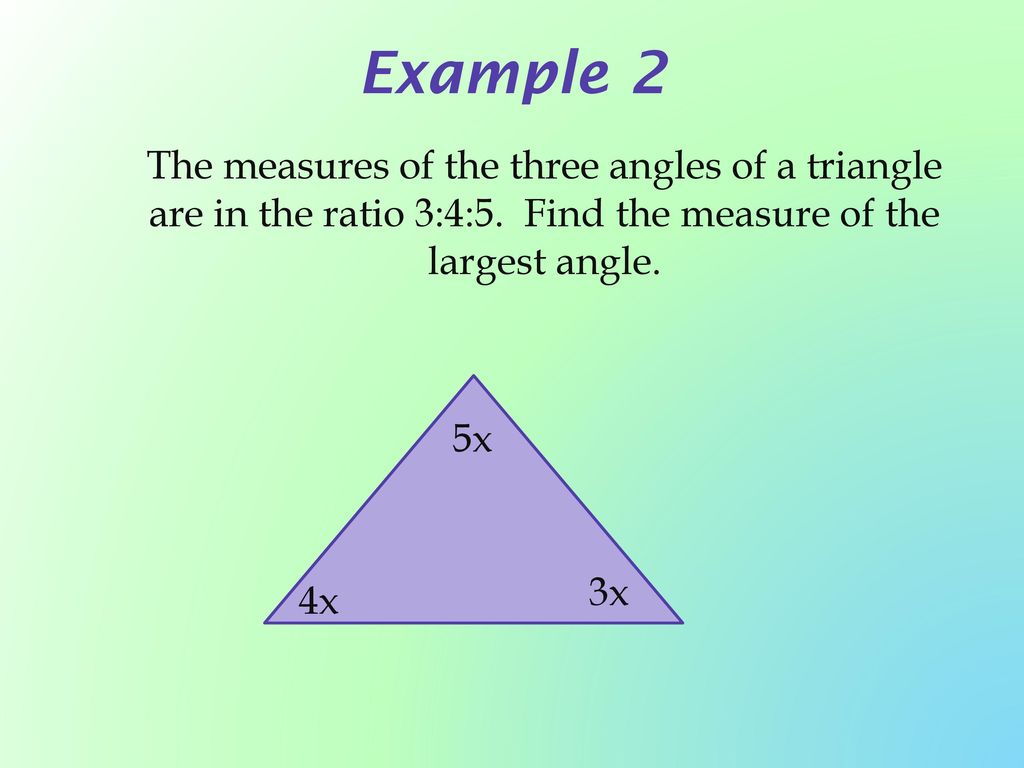



7 1 Triangle Application Theorems Ppt Download
For any right triangle, there are six trig ratios Sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot) Here are the formulas for these six trig ratios Given a triangle, you should be able to identify all 6 ratios for all the angles (except the right angle) Let's start by finding all 6 ratios for angle AThe ratios of corresponding sides are 6/3, 8/4, 10/5 These all reduce to 2/1 It is then said that the scale factor of these two similar triangles is 2 1 The perimeter of Δ ABC is 24 inches, and the perimeter of Δ DEF is 12 inches When you compare the ratios of the perimeters of these similar triangles, you also get 2 14 5 Any triangle whose sides are in the ratio 345 is a right triangle Such triangles that have their sides in the ratio of whole numbers are called Pythagorean Triples There are an infinite number of them, and this is just the smallest See pythagorean triples for more information




Q3b Sides In The Ratio 3 4 5 Draw Triangles Specified Below Each Of Perimeter 10




Side Ratios In Right Triangles As A Function Of The Angles Article Khan Academy
The 345 triangle is the best way I know to determine with absolutely certainty that an angle is 90 degrees This rule says that if one side of a triangle measures 3 and the adjacent side measures 4, then the diagonal between those twoLet the measure of the angles be 3x, 4x, 5x We know that, the sum of the angles of a triangle =180o So, 3x4x5x=180o ⇒12x=180o ⇒x= 180o 12 ⇒x=15o Therefore, Smallest angle = 3xThe angles of a triangle are in the ratio 3 4 5 Find the smallest angle Medium Open in App Solution Verified by Toppr Given that, The ratio of angles of a triangle = 3 4 5 Let the angle,
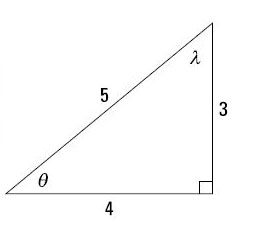



Use 6 Different Ratios Of A Right Triangle Dummies




African Creation Energy The Ptah Horus Pythagoras Theorem The African Origin Of The Pythagorean Theorem
The sides of a triangle are in the ratio 345 what is the length of each side if the perimeter of the triangle is 90cmYou can absolutely have a right triangle with short sides 4 and 5, but the hypotenuse would have to be the square root of 41, which is approximately 64 Think of




3 Draw Triangles Specified Below Each Of Perimeter 18 Cent Scholr




If The Sides Of A Triangle Are In The Ratio 3 4 5 Prove That It Is Right Angled Triangle Maths Triangles Meritnation Com




Pythagorean Triangle With Side Lengths Having The Ratio 3 4 5 The Download Scientific Diagram




Resources 3 4 5 Principle




Properties Of The Ratio Of Areas Of Triangles Geogebra




The Three Angles Of A Triangle Are In The Ratio 3 4 5 Then The Angles Are Passingmarks




The Angles Of A Triangle Are In The Ratio 3 4 5 Find The Smallest Angle In Degrees And The Youtube



Cosecant Cosecant Function Csc
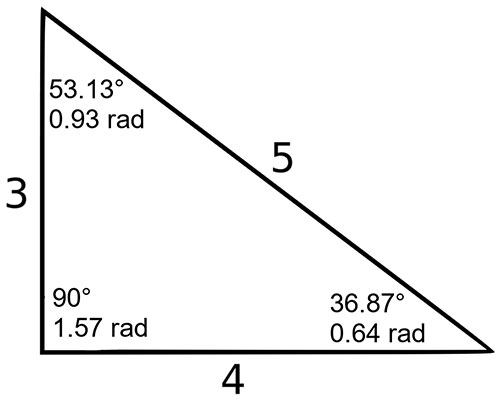



3 4 5 Triangle Angles Sides How To Solve Full Lesson
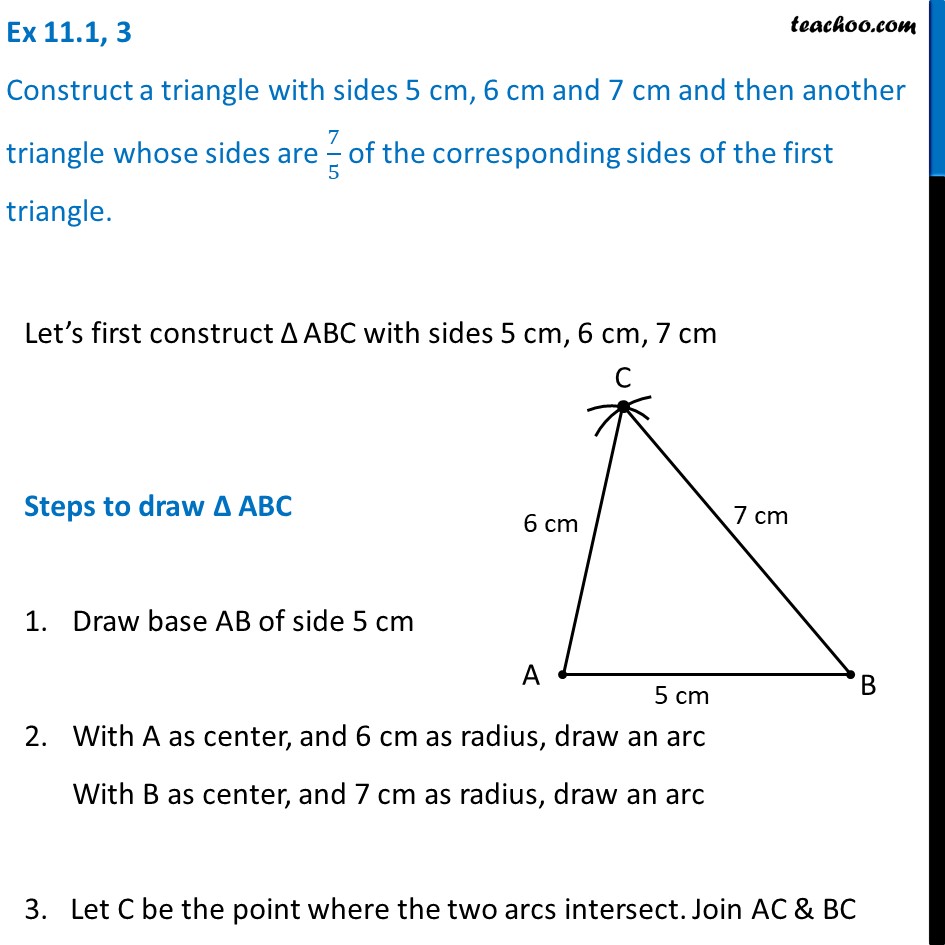



Ex 11 1 3 Construct A Triangle With Sides 5 Cm 6 Cm And 7 Cm



1




3 4 5 Right Triangles Explanation Examples



Construct A Triangle With A Given A Perimeter In The Ratio 2 3 4 Technical Graphics



The 3 4 5 Triangle



Construct A Triangle Abc Having Perimeter 12 Cm And Angles In The Ratio 3 4 5 Mathematics Topperlearning Com Gyq8yb6tt




Ml Aggarwal Solutions For Class 9 Maths Chapter 16 Mensuration Access Pdf



The Lengths Of The Sides Of A Triangle Are In The Ratio 3 4 5 And Its Perimeter Is 144 Cm Find The Area Of The Triangle And The Height Corresponding To The Longest




5 4 Two Poles Of Heights 6 M And 11 M Stand On A Plane Math




The Golden Ratio In Amalgam Of 1 2 5 Triangle And 3 4 5 Triangle Download Scientific Diagram




Properties Of 3 4 5 Triangles Definition And Uses Video Lesson Transcript Study Com



1




Q3 The Angles Of A Triangle Ar Lido
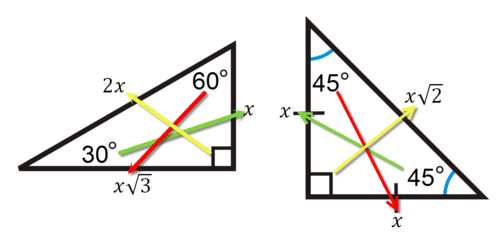



Special Right Triangles Read Geometry Ck 12 Foundation
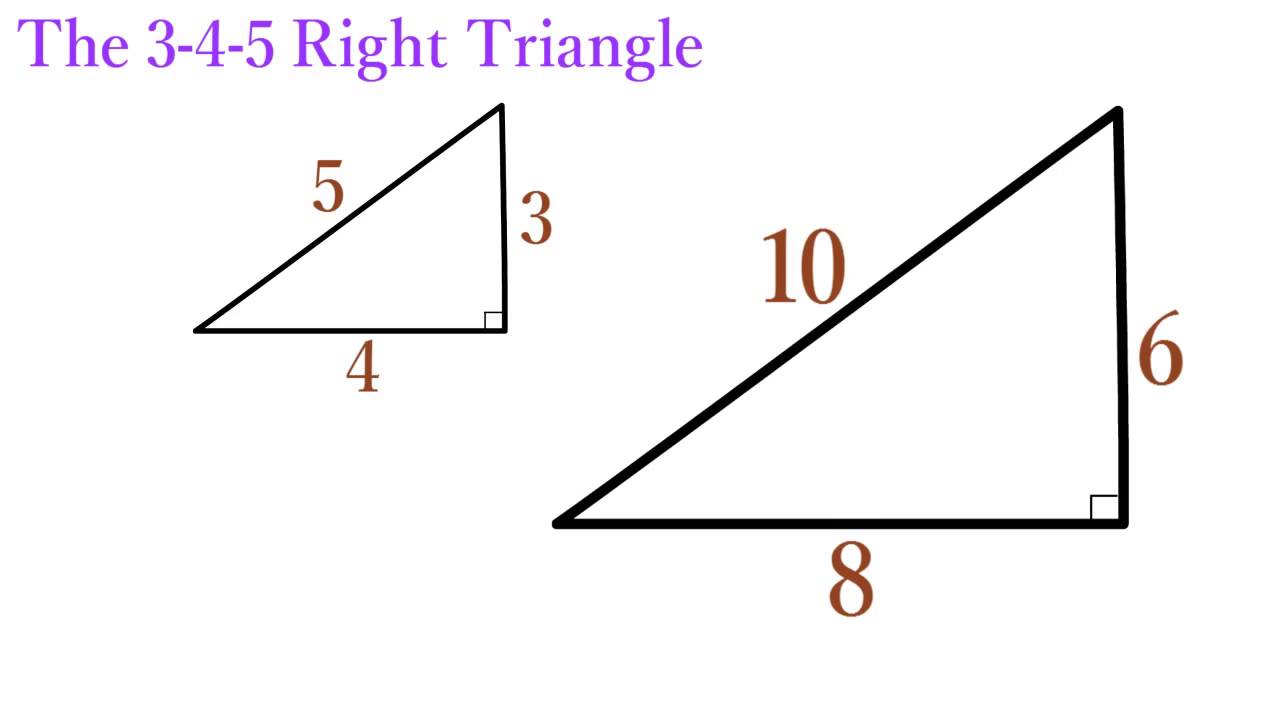



Lesson 12 The 3 4 5 Right Triangle Simplestep Learning Youtube




Vector Circle Arrows Infographic Cycle Diagram Graph Presentation Chart Business Concept With 3 4 5 6 7 8 Option Part Step Process Ecology Nature Flower Triangle Timeline Puzzle Jigsaw Stock Illustration Download Image Now Istock
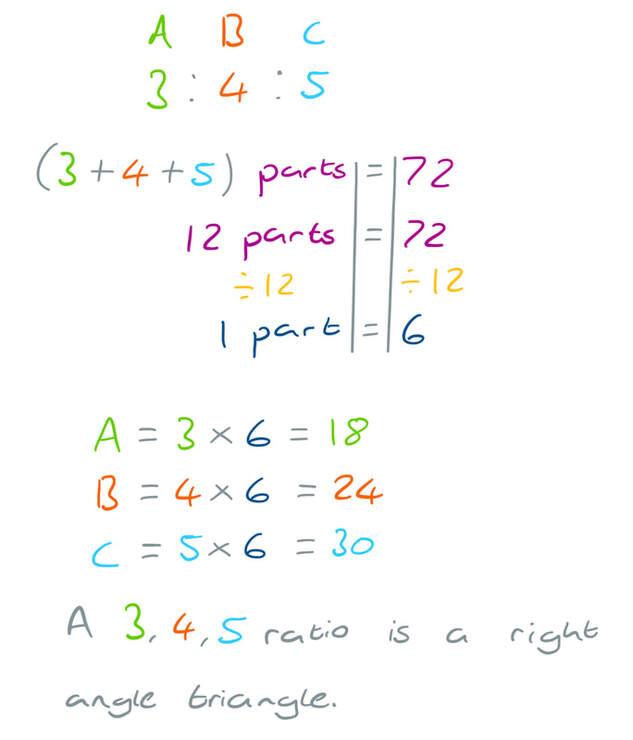



Q8 Answers Paper 1 June 18 Edexcel Gcse Maths Higher Elevise




Special Right Triangle Wikipedia




The Length Of The Sides Of A Triangle Are In The Ratio 3 4 5and It S Perimeter Is 60cm Find It S Area Brainly In
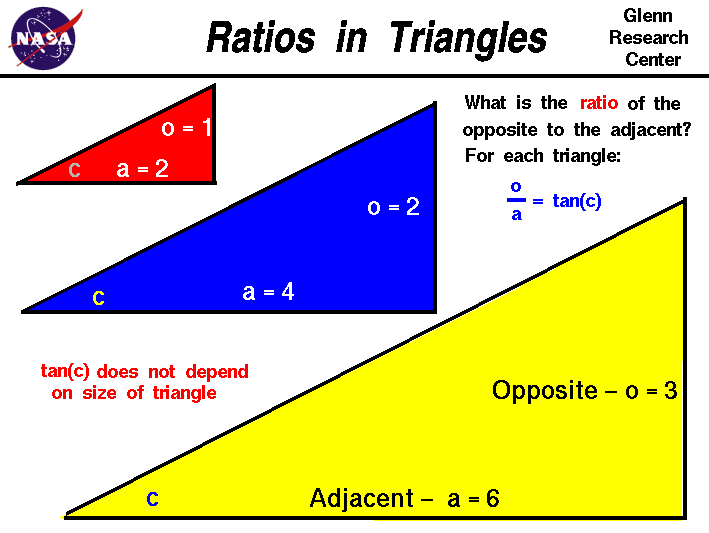



Ratios In Triangles




The Sacred Triangle 3 4 5 Sacred Geometry Symbols Sacred Sacred Geometry
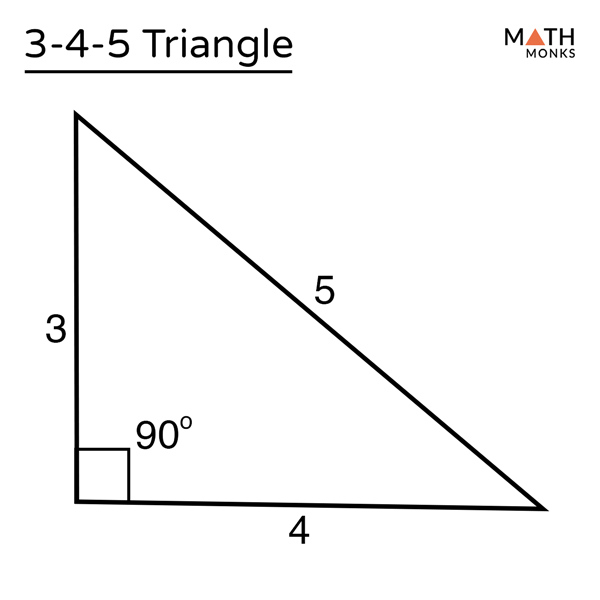



3 4 5 Triangle Properties Formula Examples




Problem Solving With Geogebra Construction Problems For Gcse Mathematics



Is Every Right Triangle A Rationed 3 4 5 Triangle Quora
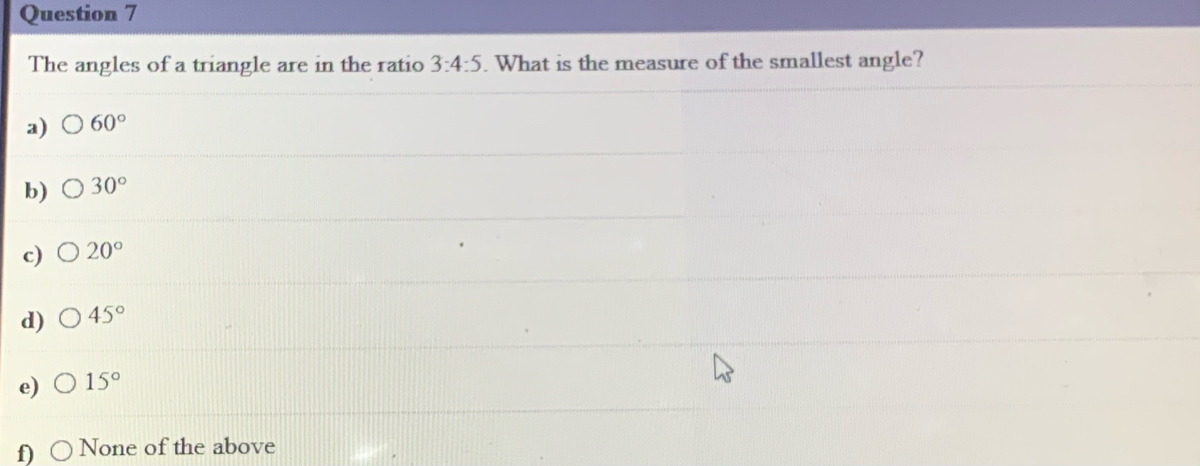



Answered Question 7 The Angles Of A Triangle Are Bartleby




The Golden Ratio In Amalgam Of 1 2 5 Triangle And 3 4 5 Triangle Download Scientific Diagram




Assignment 9 Pdfthe Sides Of A Triangle Are In The Ratio 3 5 7 And It Acirc




1 If The Angles Of Triangle Are In Ratio 5 6 9 Then What Is The Difference Between The Greatest And The Maths Linear Equations In One Variable Meritnation Com




The Ratio Of The Angles Of A Triangle Is 3 4 5 What Is The Difference Of The Bi



Solution Hi I 39 M Having A Bit Of Trouble Do You Think You Could Help The Angles Of A Triangle Are In The Ratio 3 4 5 If The Shortest Side Has A Length Of
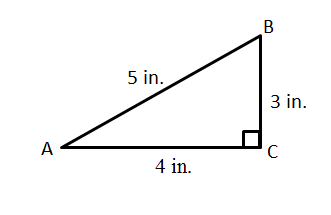



The 6 Trig Ratios
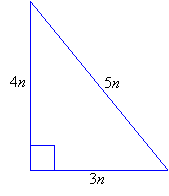



3 4 5 Right Triangles Worked Solutions Examples Videos



Special Right Triangle 30 60 45 45 37 53 Elearning




3 4 5 Triangle Definition Math Open Reference
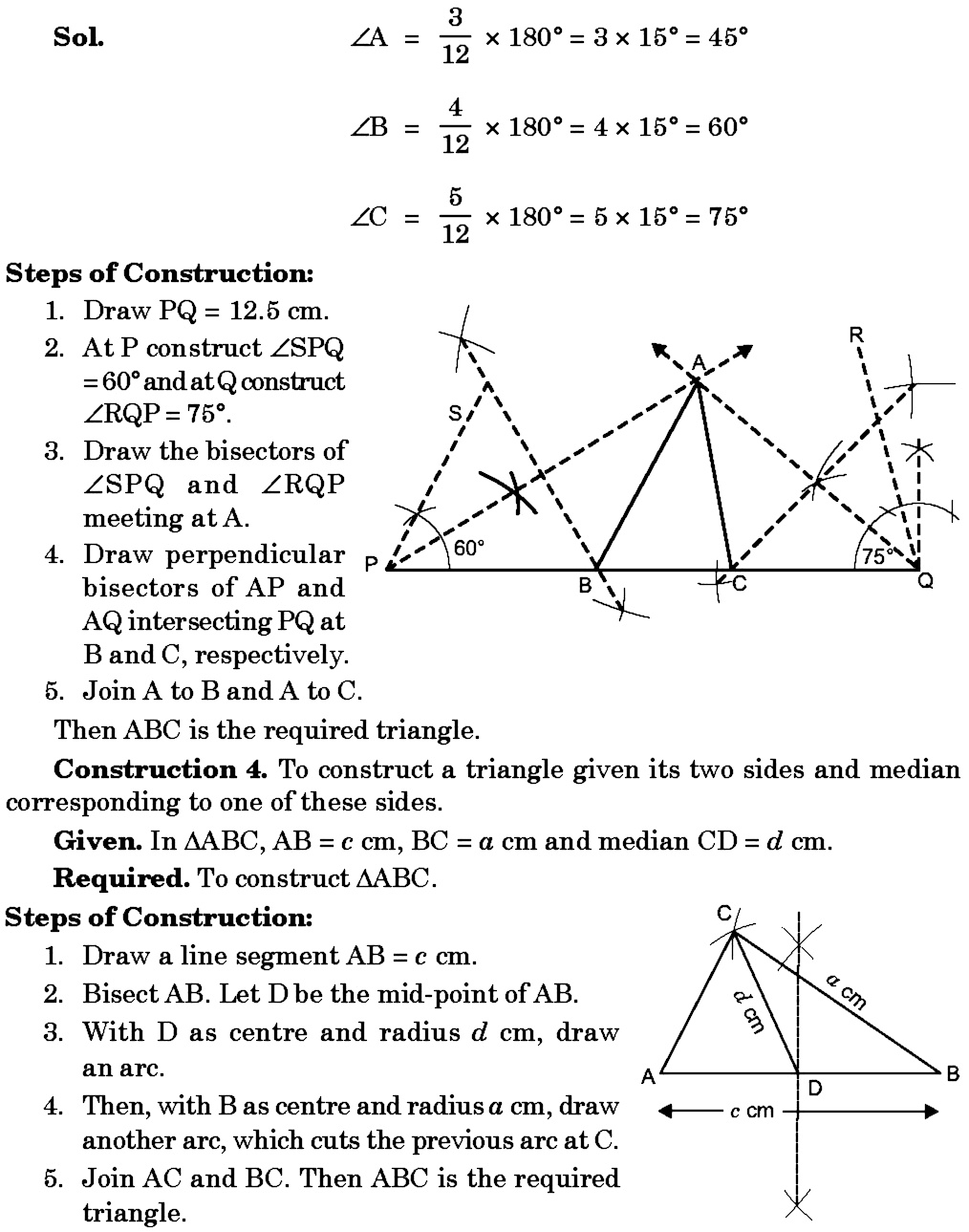



Example 8 Construct A Triangle Having Its Perimeter 12 5 Cm And The Ratio Of The Angles As Tex 3 4 5 Tex Most Important Hots Snapsolve
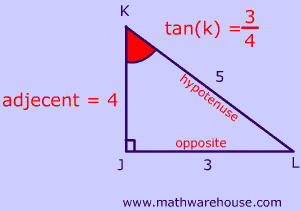



Sine Cosine And Tangent Ratios Of A Triangle How To Write The Trig Ratios Of Right Triangles




The Sides Of A Triangle Abc Are In The Ratio 3 4 5 If The Perimeter Of Triangle Abc Is 60 Then Its Lengths Of Sides Are
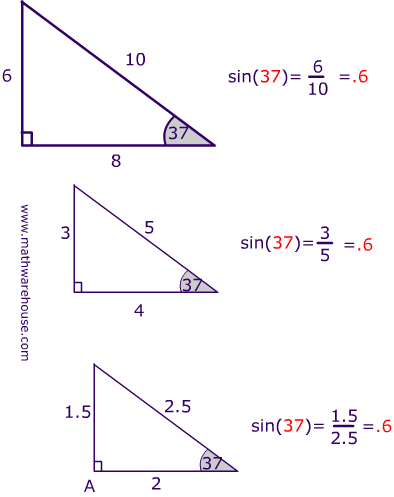



Pictures Of 3 4 5 Right Triangles Free Images That You Can Download And Use




Construct A Triangle Mnp Whose Perimeter Is 15 Cm And Whose Sides Are In The Ratio 2 3 4
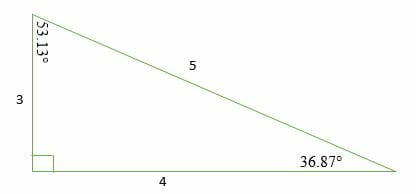



3 4 5 Right Triangles Explanation Examples




Solved The Sides Of A Triangle Abc Are In The Ratio 3 4 5 If Self Study 365




The Angles Of A Triangle Are In The Ratio 3 4 5 Find The Smallest Angle In Degree And The Greatest Angle In Radians




3 4 5 Triangle Definition Math Open Reference




Pythagorus Theorum Math Lesson 3 4 5 Triangle Youtube




Of Sidesname Of Diagonalsinterior Angle Sum Exterior Angle Sum Each Interior Angle If Regular Each Exterior Angle If Regular Ppt Download
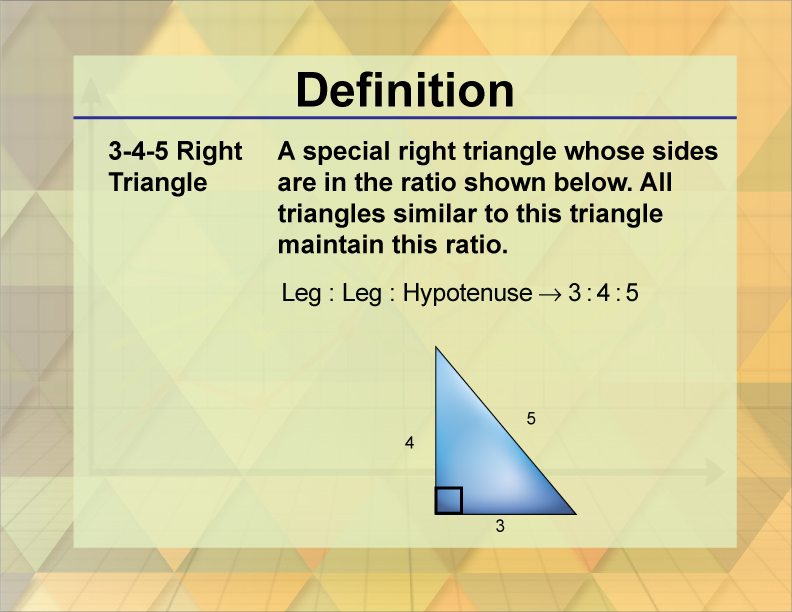



Definition Triangle Concepts 3 4 5 Right Triangle Media4math



A Triangle With Side Lengths In Ratio 3 4 5 Is Inscribed In A Circle Of Radius 3 What Is The Area Of The Triangle Quora
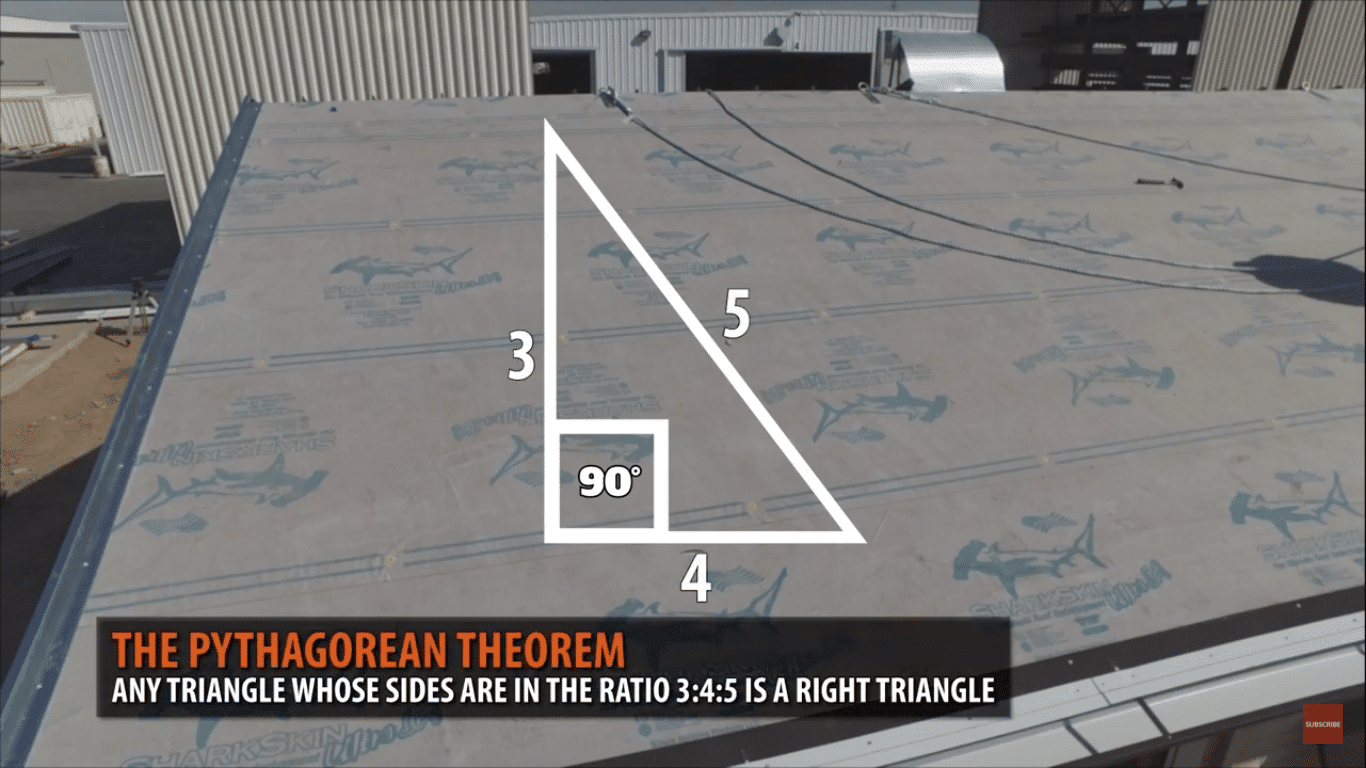



How To Square A Metal Roof The 3 4 5 Triangle Method
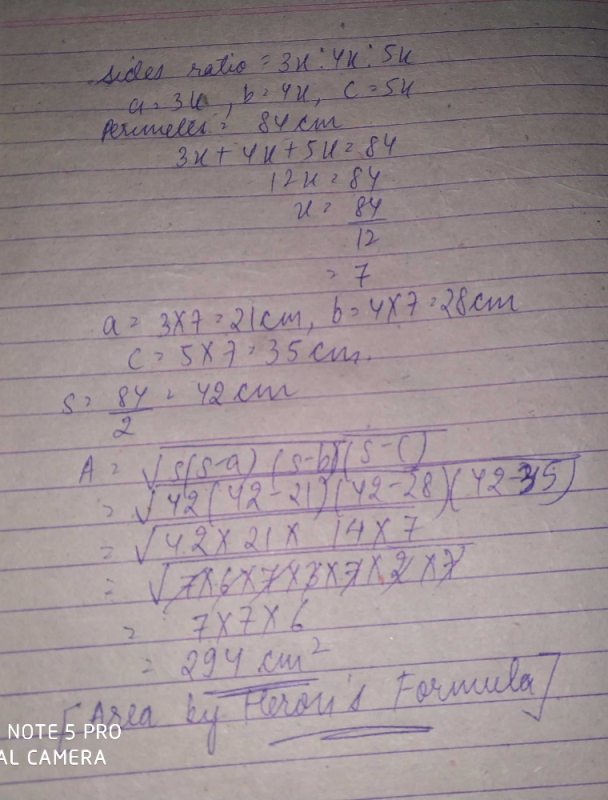



The Sides Of A Triangle Are In Ratio 3 4 5 If The Perimeter Of The Triangle Is 84 Cm Then Area Of The Triangle Is A 294cm2b 290cm2c 274cm2d 252cm2correct Answer Is Option
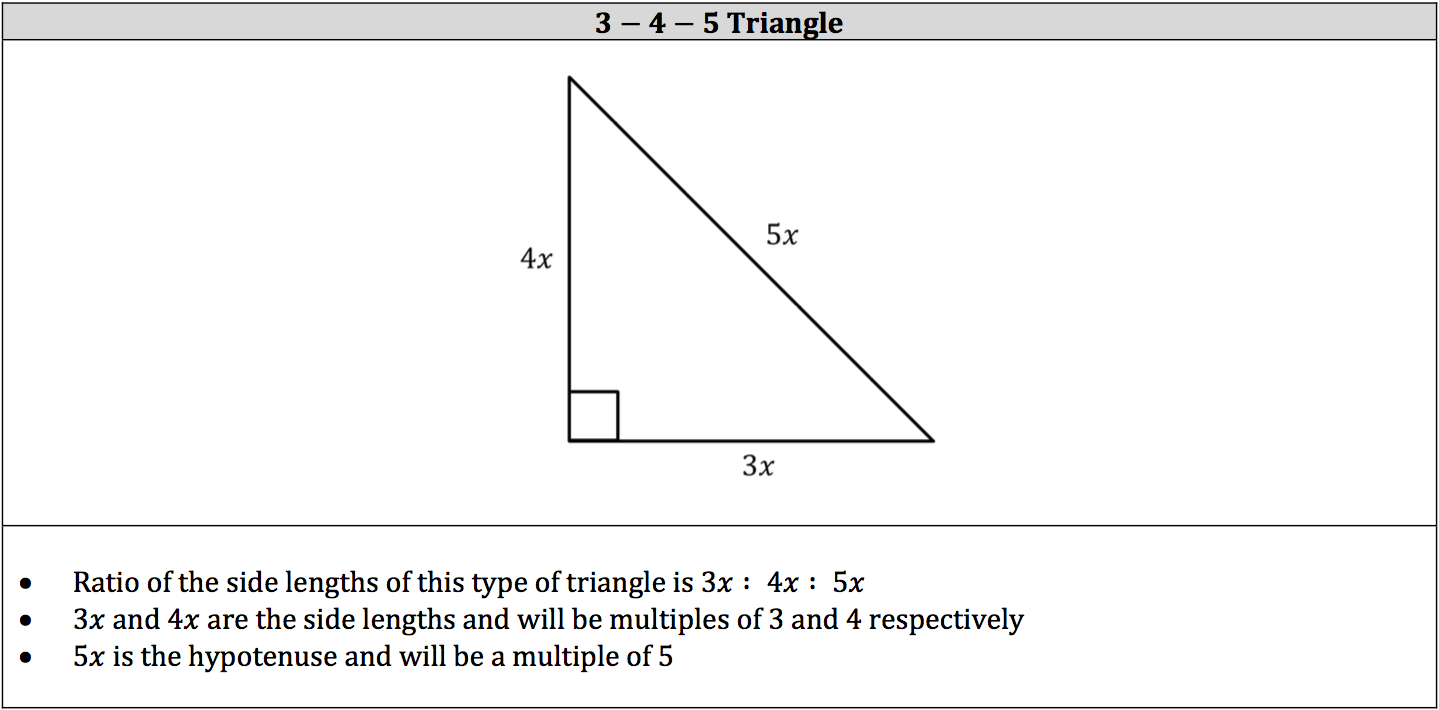



Isee Math Review Triangle Types And Rules Piqosity Adaptive Learning Student Management App



1



Solved A Wire 252 Centimeters Long Will Be Bent Into Shape Of Right Triangle Whose Sides Are The Ratio Of 3 4 5 How Long Is The Hypotenuse Of Th Course Hero




The Area Of The Triangle Is 150cm 2 Its Sides Are In The Ratio 3 4 7 What Its Perimeter Edurev Class 9 Question



View Question A Triangle Has Side Lengths In The Ratio 3 4 5 If The Perimeter Of The Triangle Is 84 Cm What Is The Length Of The Shortest Side



The Lengths Of The Sides Of A Triangle Are In The Ratio 4 5 3 And Its Perimeter Is 96 Cm Find Its Area Sarthaks Econnect Largest Online Education Community




The Angles Of A Triangle Are In The Ratio 3 4 5 Find The Smallest Angle In Degrees And The Greatest Angle In Radians




The Sides Of A Triangle Are In The Ratio 3 4 5 The Measure Of The Largest Angle Of The Triangle Youtube



A Triangular Table Whose Sides Are In The Ratio 3 4 5 And Its Perimeter Is 36 M Sarthaks Econnect Largest Online Education Community




Answered Axyzhas Side Lengths In The Ratio Bartleby
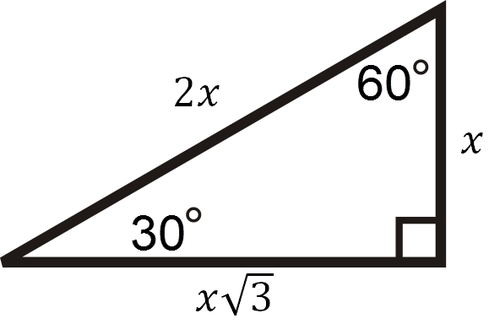



Special Right Triangles And Ratios Geometry




Solved Use An Algebraic Equation To Solve The Problem The Chegg Com




Special Right Triangles Flashcards Quizlet
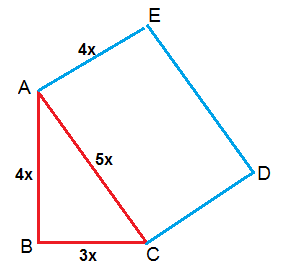



The Side Other Than Hypotenuse Of A Right Triangle Are In The Ratio Of 3 4 A Rectangle Is Described In Its Hypotenuse The Hypotenuse Being The Longer Mathematics Topperlearning Com G5ftg0aa




Using Similarity To Estimate Ratio Between Side Lengths Video Khan Academy



1




Triangle Area Higher Gcse Questions These Questions Are




Q8 Answers Paper 1 June 18 Edexcel Gcse Maths Higher Elevise



No comments:
Post a Comment